Introduction

Consider an mathematical expression 1+2*3. The same expression can be interpreted as (1+2)*3 and 1+(2*3), but only one of them is an accurate representation. Because of the fundamental arithmetic rules, we know that * has higher precedence and hence the second interpretation i.e, 1+(2*3) is accurate. But how exactly can we write an algorithm to compute the correct representation given an expression.

The parse tree

Parsers generally convert a string(or a list of tokens) into a tree like structure. Such a tree is commonly referred to as an Abstract Syntax Tree or AST for short. The interpretation for our expression 1+2*3 i.e 1+(2*3) and (1+2)*3 can be represented as per the following diagram:

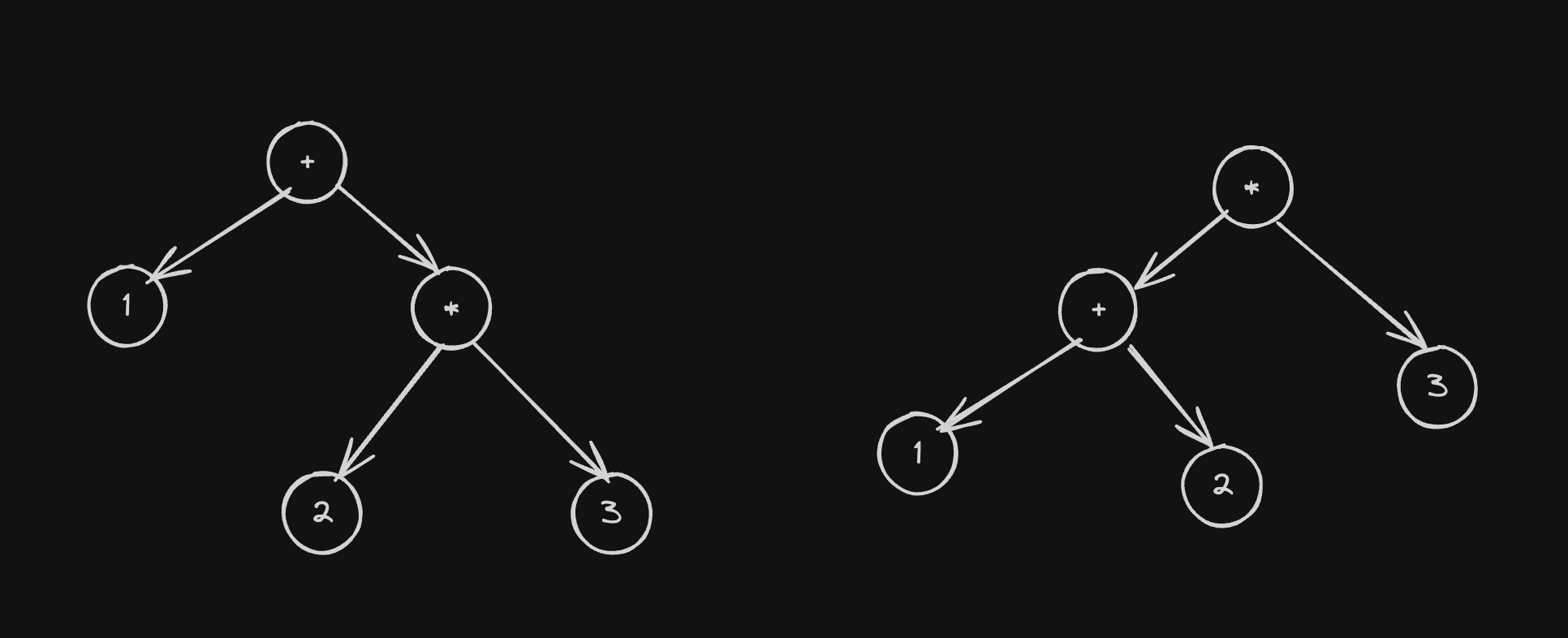
The algorithm

The final parse tree will have a root expression(+ in the 1+(2*3)) and an LHS (1 in 1+(2*3)) and an RHS (2*3 in 1+(2*3)). Note that the LHS and RHS can themeselves be trees, thus the tree structure of the parsed expression.

There are a handful of different algorithms to do precedence parsing, like Shunting Yard and Pratt Parsing algorithm. Out of all of these, the most ubiquitous and flexible algorithm is pratt parsing. The algorithm is fundamently based on an iterative construction of an expression and a recursive construction of the RHS.

Let’s consider our expression 1+2*3

For all expressions the first parse is going to be a number (this will change later, but let’s just keep things simple for now). For sake of a unified terminology, I will call this
prefix parsing(you can think of the function that performs this parsing is called parsePrefix). Another term that is going to be used is the right binding power. Right binding power
is the precedence of the last encountered op. An obvious question at this point would be to ask why such a term is even required, what is the relevance of the RBP?

Let us assume we parsed the LHS of a particular operation as 1 and +, the RHS parsed here would be 2*3. If the LHS on the other hand is 1+2 and *, the RHS parsed here is 3. Let’s compute the precedence of the current op: + in the first case(let’s give the number 1 for this) and *(let’s give a precedence of 2 for this) in the second case. The RHS of the first expression contains an op of * with precedence 2. And the LHS of the second expression contains an op +(precedence 1).

From inspection, the precedence of the earlier nodes in topological order should be greater than the the precedence of the later nodes. Hence in our case the first expression (topological order is [1,2,3,*,+]) and their precedences are [0,0,0,1,2] (Note that this array is sorted in ascending order).

So the right binding power is important because while recursively constructing the tree we need to satisfy the following condition: the right hand sides/ the topologically sooner ops should have a precedence greater than the topologically latter op’s precedence. If that’s not the case, then we need to abort constructing a new child for the parsed expression and should create a new root node with the currently parsed expression as its LHS.

To make this more concrete, consider the expression 1*2+3. The first parse gives the number 1 and the op is *. Initial precedence is 0 and the op precedence is 2, hence we can construct a child for this op, since the earlier constraint is satisfied. Hence we construct the RHS for the leftover expression 2+3. Again the number 2 is parsed and the op is +. The current RBP is 2 and hence constructing a child with the + op will not satisfy our constraint.
Hence we abort the construction and just return 2. The LHS is now (1*2) and the + expression becomes the new root op (Note that topological order is maintained), the leftover expression is just 3 and the prefixParse is called and 3 is returned as the RHS, hence giving the final expression as (1*2)+3.

Putting this into code:

fn parseInfix(lexer: *Lexer, lhs: *ast.TreeNode, allocator: std.mem.Allocator) !*ast.TreeNode {
    if (lexer.currentToken) |currentToken| {
        _ = Lexer.nextToken(lexer);
        const op = currentToken.Operator; // assert that token is an operator
        const derefedToken = currentToken.*;
        var rhsOpt = switch (derefedToken) {
            .Operator => try parse(lexer, allocator, getPrecedence(currentToken)), // operator is used to calculate the precedence and the rhs is recursively constructed
            .Integer => null,
            .Invalid => null,
            .LParen => null,
            .RParen => null,
        };
        if (rhsOpt) |rhs| {
            var parsed = try allocator.create(ast.TreeNode);
            parsed.BinOp = ast.BinOpStruct{
                .lhs = lhs,
                .rhs = rhs,
                .op = op,
            };
            return parsed;
        } else {
            return lhs;
        }
    } else {
        std.debug.assert(false);
    }
    return lhs;
}

fn parsePrefix(lexer: *Lexer, allocator: std.mem.Allocator) !*ast.TreeNode {
    var tokenOpt = lexer.currentToken;
    var prefixParsed = try allocator.create(ast.TreeNode);
    if (tokenOpt) |token| {
        if (@as(ast.TokenType, token.*) == ast.TokenType.Integer) {
            prefixParsed.* = ast.TreeNode{ .Integer = token.Integer }; // simple function, checks if the prefix is an integer, parses and returns, all other lines are just sanity checks
        } else {
            unreachable;
        }
        return prefixParsed;
    } else {
        return ParserError.ParseError;
    }
}


fn parse(lexer: *Lexer, allocator: std.mem.Allocator, currentPrecedence: u32) (ParserError)!*ast.TreeNode {
    var parsed = try parsePrefix(lexer, allocator); // prefix is parsed
    const peekedTokenOpt = lexer.peekToken();
    if (peekedTokenOpt) |peekToken| {
        var precedence = getPrecedence(peekToken);
        while ((precedence > currentPrecedence)) { // iterative construction of the lhs
            const nextTokenOpt = Lexer.nextToken(lexer);
            if (nextTokenOpt) |_| {
                parsed = try parseInfix(lexer, parsed, allocator); // infix is parsed
            } else {
                return parsed; // null => lexer tokens are done
            }
        }
    } else {
        return parsed; // null => there are no more tokens to parse, hence return
    }
    return parsed; // while loop exits
}

Conclusion

I cannot count the number of times I have forgotten how pratt parsing works and hence this blog on my interpretation of the algorithm. The best way to understand the algorithm in my opinion is to consider the topological constraint and tree reconstruction and the morphological structure of the code, namely the elements: the iterative LHS construction(while loop) and the recursive RHS construction(parse call in parseInfix).

The code for a more feature rich pratt parser(supporting unary negative and brackets) is implemented in these github repos:

1. Go
2. Zig

References

• Pratt parsing original paper url