How to do matrix multiplications via reshapes and mulaccs? Ever since reading through the tinygrad implementation of matmul, I have been trying to understand how to do it functionally. This is the code from tinygrad:

  def dot(self, w:Tensor, acc_dtype:Optional[DTypeLike]=None) -> Tensor:
    n1, n2 = len(self.shape), len(w.shape)
    assert n1 != 0 and n2 != 0, f"both arguments to matmul need to be at least 1D, but they are {n1}D and {n2}D"
    if (L:=self.shape[-1]) != (R:=w.shape[-min(n2, 2)]): raise AssertionError(f"shapes {self.shape} and {w.shape} cannot be multiplied ({L} != {R})")
    x = self.reshape(*self.shape[0:-1], *[1]*min(n1-1, n2-1, 1), self.shape[-1])
    w = w.reshape(*w.shape[0:-2], *[1]*min(n1-1, n2-1, 1), *w.shape[-min(n2, 2):]).transpose(-1, -min(n2, 2))
    return (x*w).sum(-1, acc_dtype=acc_dtype).cast(least_upper_dtype(x.dtype, w.dtype) if acc_dtype is None else acc_dtype)

  def matmul(self, x:Tensor, reverse=False, acc_dtype:Optional[DTypeLike]=None) -> Tensor:
    return x.dot(self, acc_dtype=acc_dtype) if reverse else self.dot(x, acc_dtype=acc_dtype)

Lets run through this program line by line for two different input pairs. 2*3 3*2 , n1 = 2, n2 = 2; L = 3, R = 3 2*3 2*3, n1 = 2, n2 = 2; L = 3, R = 2 The assertion in the third line in the dot function fails in the second case. Last dimension of the first, and the last to last dimension of the second. The way to probably think of this is that the last two dimensions are cols and rows, all the others are some form of batching.

Lets test this hypothesis in numpy. The following numpy repl is self explanatory:

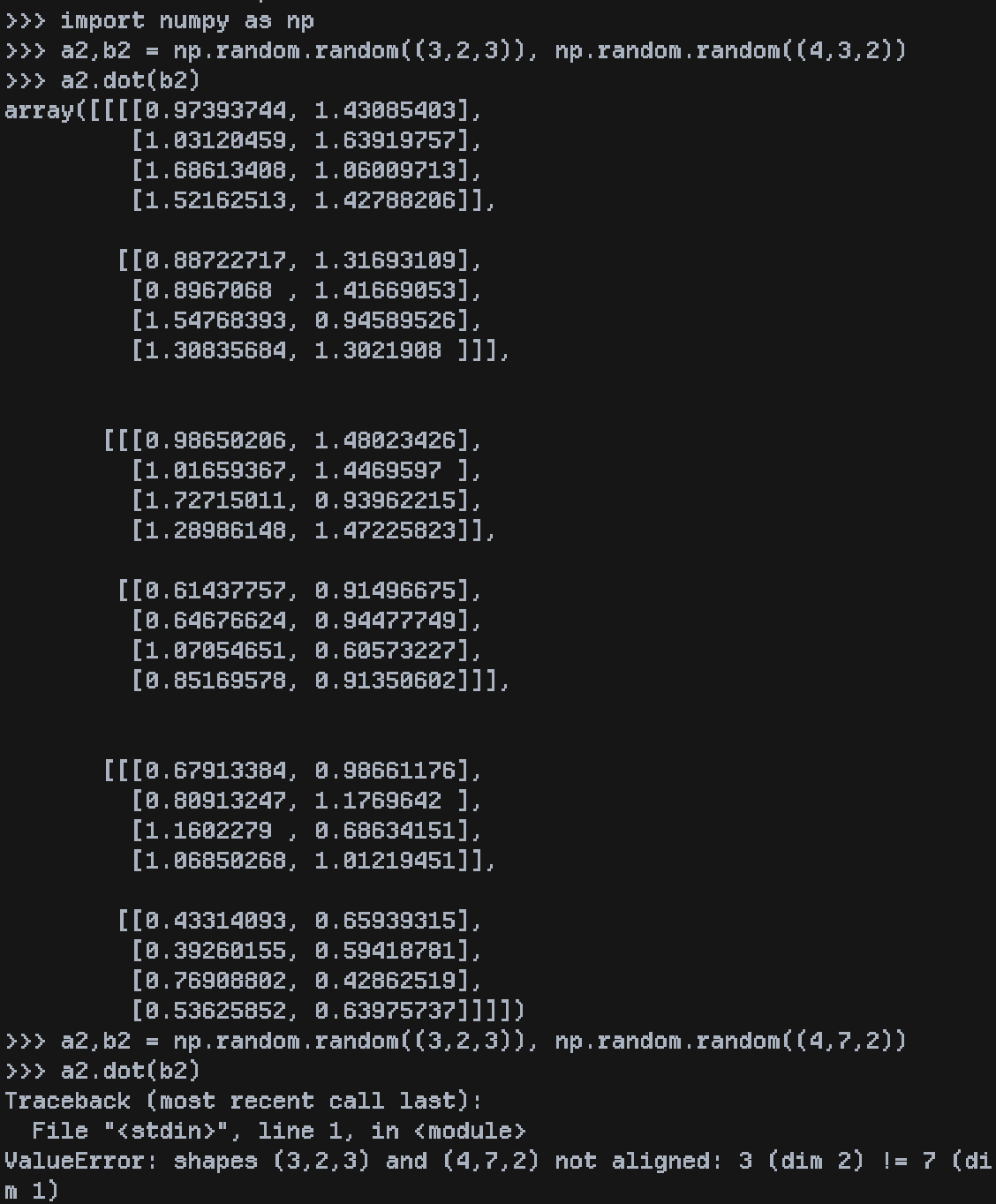
The value error because of the mismatched dimension corresponds to line 3 in the dot function.

Now there are two lines of reshapes and transposes. For the sake of the rest of the article, I will call them as movement operations. Movement operations offer an alternate view to the existing array. Plus in tinygrad(at least in the initial versions) the tensor housed a numpy array, and the operations ended up boiling down into numpy operations. Now to address the reshapes that are being done here. For this (and this took me maybe a couple of hours to understand), we will look a 2*2 numpy dot output. Numpy dot for 2D 2D array inputs is a matrix multiplication. Tinygrad replicates this behaviour(if you look at the matmul function). Now lets look at how 2D matrix multiplication actually gets computed.

[[1,2], [3,4]] @ [[-1,-2],[-3,-4]]

# We perform some element wise products and we add them up in a matmul
[1*-1 + 2*-3] [1*-3 + 2*-4]
[3*-1 + 4*-3] [3*-3 + 4*-4]

# Lets look at them as some sort of element wise multiplications.

[1 2] . [-1 -3] | [1 2] . [-3 -4]
[3 4] . [-1 -3] | [3 4] . [-3 -4[]

We can observe that there is some kind of replication here of the rows of both the matrices. the rows [1 2] and [3 4] are replicated horizontally and the rows [-1 -3] and [-3 -4] are replicated vertically. This sort of a replication is a behaviour of numpy called broadcasting.

How can we utilize this broadcasting and write this as a numpy elementwise product? For horizontal broadcasting (or broadcasting along a numpy axis of 1 or the second to last dimension). To call such a broadcasting the easiest way is to make the dimension that you need to replicate as the additional unary dimension in the axis’s position. So here we will perform the following operation:

a = np.array([[1,2], [3,4]])
a_reshaped = np.reshape(a, (2,1,2))

Now look at the other rows, [-1 -3] and [-3 -4].Now these are not the original rows of our matrix, its a transpose or an axis swap of some sort. Lets first broadcast it in the corresponding direction (vertical) or the numpy axis 0. Hence we add the additional dimension of 1 to the older array, again no transposition as of now.

b = np.array([[-1,-2], [-3,-4]])
b_reshaped = np.reshape(b, (1,2,2))

Now let’s do a transpose. Transpose basically swaps the rows and cols axis. Now dot/matmul is not a 2D tensor anymore. It can be an N-D tensor. In such cases the other dimensions are assumed to be some batching and matmul is done for the 2D tensor in the innermost dimensions. Hence we swap the last and the second to last dimension of this array.

b_reshaped_transposed = b_reshaped_transposed.swapaxes(-1,-2)

Now lets perform an elementwise multiplication between our b_reshaped_transposed and a_reshaped arrays. The following value is observed:

array([[[ -1,  -6],
        [ -2,  -8]],

       [[ -3, -12],
        [ -6, -16]]])

Now we have our elementwise multiplies, we just need so sum up in the right axis. In this case the axis is the last one(represented as -1). So lets perform our last sum operation

matmul_result = (a_reshaped * b_reshaped_transposed).sum(-1)

You can verify this is the same result that np.dot gives us. The only hardcoded values till here is the reshape. Now we need to adapt this to higher dimensions, i.e when batching is involved.

Let’s follow our old logic, add a dimension prior to the last dimension:

a_reshaped2 = a.reshape(*a.shape[0:-1],*[1],a.shape[-1])
assert np.allclose(a_reshaped2, a_reshaped)

This assertion doesn’t get triggered. Hence we are on the right track. Now for b, we need to add a dimension prior to my rows and cols, i.e maintain the last 2 dimensions at the end, then a 1 and then have the batching dimensions before that:

b_reshaped2 = b.reshape(*b.shape[0:-2],*[1],*b.shape[-2:])
assert np.allclose(b_reshaped2, b_reshaped)

Now this leads to our dot implementation:

def mydot(a,b):
    a_dims,b_dims = len(a.shape), len(b.shape)
    assert a_dims >= 2 and b_dims >= 2
    assert a.shape[-1] == b.shape[-2]
    a1 = a.reshape(*a.shape[0:-1],*[1],a.shape[-1])
    a2 = b.reshape(*b.shape[0:-2],*[1],*b.shape[-2:]).swapaxes(-1,-2)
    return (a1*a2).sum(-1)

Now we have almost replicated tinygard’s matmul. What remains is handling the 1d tensors(and that is being handled with the extra if conditions and mins in tinygrads code).